[Paper review]SpinQuant: LLM quantization with learned rotation

기존 문제점

---

• Outlier로 인한 양자화 오류 증가
  • quantization 범위의 과도한 확장으로 reconsturction error이 발생. 이로 인한 모델 성능 저하 현상을 해결하고자 제안.

LLaMA-2 7B 모델의 특정 레이어 activation 분포가 kurtosis 200이 넘을 정도로 꼬리가 길고, 양자화 오차가 매우 큰 것을 확인할 수 있다.

• Random Rotation만으로는 성능 편차가 매우 큼
  • Outlier 완화를 위한 연구 중 random orthogonal or Hadamard matrix를 곱해 activation/weight 분포를 섞는 방식은 양자화 후 성능 변동이 크게 나타남

 

LLaMA-2 7B 모델을 W4A4(4비트 가중치, 4비트 활성화)로 양자화했을 때, 랜덤 floating-point 회전 사용 시 최대 13%p, 랜덤 Hadamard 회전 사용 시 최대 6%p 편차가 발생함

320x100

 

해결을 위한 핵심 아이디어

---

학습 가능한 회전 행렬 도입 (weight & activation의 값의 분포 균일화)

$R*R^T=I$와 같은 상황을 통해서 기존 값 복원이 가능하다는 점을 이용

1. 양자화 손실을 직접 최소화하는 회전 학습 (Cayley SGD)

• 회전 행렬 R
  • 랜덤으로 고정 + quantization loss를 직접 최적화하도록 학습
  • 정규 직교행렬, Cayley 변환 기반 SGD로 업데이트
  $$ \underset{{R∈Stiefel}}{min}L_Q(R_1,R_2∣W,X) $$$$ Y=G'-G'^T,\\ G':=GR^T - \frac1 2RR^TGR^T $$
  • 네트워크 출력은 그대로 유지하며 양자화 후 오차가 최소화되는 최적의 R을 찾는다.
  • 학습된 R’을 사용해 성능 편차를 감소시키고 안정적으로 양자화 성능 개선
• $$ R' = \Delta R(Y)R:=(I-\frac{\alpha}{2}Y)^{-1}(I+\frac\alpha 2Y)R $$

 

2. 회전행렬 통합 및 선택적 Hadamard 회전 활용

• R1 = 임베딩 후 Residual stream 회전
  • 토크나이저 임베딩 $X$에 $R_1$을 곱하고, 이후 Attention / FFN 연산 후 다시 $R_1^T$를 곱함
  • 회전 행렬은 FP 네트워크 출력에 영향을 주지 않으며, outlier 완화 효과만 남는다.
  • outlier 제거 + fully-connected layer 입력 activation 양자화 완화
• R2 = Attention block 내 값 및 out-projection 회전
  • 멀티헤드 어텐션에서, V를 회전하고, Attention 최종 출력에 역회전 $R_2^T$을 곱함
  • Attention K-V cache 양자화 시에도 outlier가 줄어들어 더 낮은 bit로도 성능 저하를 막음
• R3, R4 = Hadamard online 회전
  • 더 극단적인 저비트 activation/cache 양자화를 위해, FFN 내부와 KV cache 내부에서 온라인 Hadamard 회전을 추가 사용
  • Hadamard 행렬 = ±1 값만 가짐
    • Fast Hadamard Transform (FHT)를 이용해 효율적으로 계산 가능
    • 각 단계에서 outlier 추가 억제
• SpinQuant_no_had
  • $R_1, R_2$만 학습하여 최종 가중치에 병합한 뒤 추론 시 추가 연산 없이 양자화된 가중치만 교체하여 사용
• SpinQunat_had
  • 학습 가능한 회전 $R_1, R_2$외에 극저비트 activation/cache를 위해 $R_3, R_4$ 같은 Hadamard 회전도 추가 적용

 

728x90

정리

---

양자화 하기 전에 Rotation matrix를 통해서 outlier 값 분포 완화

• $R^⊤R=I$: FP 상태(양자화 없이)에서는$R^T(Rx)=x$이므로 “회전→역회전”이 완전한 항등(Identity) 연산이 됩니다.
• $R^⊤(R x)=x R^\top \bigl(R\,x\bigr) = x$
• 양자화(quantize) 시점:

 

 

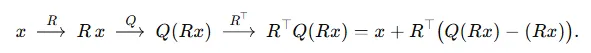
여기서 $\underbrace{Q(Rx) - (Rx)}_{=e}$는 피할 수 없는 “양자화 오차”이고, 역회전해도 영(0)이 되지는 않습니다.

• 따라서,
  1. FP 네트워크만 통과할 때는 “회전→역회전”이 정확히 $x$를 복원하므로 원래 성능이 전혀 바뀌지 않음.
  2. 양자화된 네트워크 통과 시 “회전된 값이 양자화→역회전” 과정을 거치며 양자화 손실($e$)이 남아서, 최종 복원값 $\hat{x}$는 $x$와 차이가 생김.
  3. 하지만 회전 전에 분포를 잘 재구성해두었기 때문에 원래라면 한 축에 몰렸을 아웃라이어가 여러 축으로 분산되고, 그 결과 $∥e∥$가 “회전 없이 양자화했을 때의 오차”보다 작아져, 최종 $\|\hat{x}-x\|$가 줄어듦.

결론적으로,

• 회전 행렬을 곱해도 양자화 오차가 0이 되진 않지만,
• 회전 → 양자화 → 역회전 과정을 통해 “양자화 손실”이 보다 고르게(등방성에 가깝게) 퍼지므로,
• 전체적인 재구성 오차가 작아져서 저비트 양자화 시에도 원래 모델 성능을 최대한 보존할 수 있게 됩니다.

 

 

결과

---

1. 정확도: SpinQuant_no had는 W4A8/W4A8KV8 양자화 시 FP 대비 1–3%p 격차로, 기존 RTN/GPTQ 등의 10%p 이상 격차를 크게 줄임. SpinQuant_had는 극단적 W4A4/KV4 환경에서도 FP 대비 2–4%p 격차로, 종전 학습 기반 QAT 대비 15–20%p 이상 높은 성능을 달성.
2. 안정성: Cayley 최적화 회전은 무작위 회전 대비 성능 편차를 ±0.5%p 이내로 최소화하여, 일관된 결과를 보장.
3. 시스템 효율:
   • 모델 메모리 약 4× 감소 (4비트 가중치)
   • CPU 환경에서 약 3× 속도 향상, GPU에서 Hadamard 포함 시에도 오버헤드 3–8%로 매우 작음.
4. 호환성: 회전행렬 학습만으로 기존 양자화 파이프라인(GPTQ 등)과 완전히 호환되며, 가중치에 회전을 미리 흡수해 두면 별도 연산 추가 없이 즉시 추론 가능.

이처럼 SpinQuant은 “학습 가능한 회전”을 통해 LLM 양자화 시 발생하는 아웃라이어 문제를 효과적으로 완화하고, 정확도, 메모리, 속도 측면에서 모두 실질적인 이점을 제공합니다.