[Ts = 표본화 주기 / fs = 표본화 주파수]
신호의 조건 = 대역폭(frequency)이 한정적이다.
è 시간축 제한 = 주파수 무한대
è 시간축 무한대 = 주파수 제한
Sampling 과정에 대한 조건 = 신호가 가진 최고 주파수 성분의 2배(나이퀴스트율
ð 신호 사이의 간격을 충분히 벌린다.
ð 신호를 일정 간격으로 주기적 Sampling 시 해당 Sampling 값으로부터 원래 신호를 왜곡 없이 복원 가능하다.
ð 대역폭이 한정되어 있다.
이때, 일정 간격(Ts <= 1/2B)으로 거리를 충분히 벌려줘야 하는데 그렇지 않으면 주파수 축의 신호가 겹쳐 옳지 못한 내용으로 전달하게 된다.
만약, 나이퀴스트율 보다 낮은 주파수로 Sampling 시 주파수 상에서 aliasing이라는 현상이 발생해 신호 복구 시 왜곡이 발생한다.
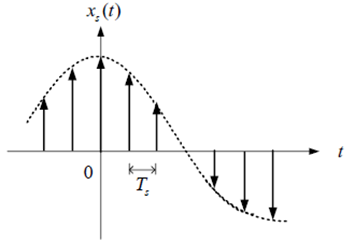
Sampling 신호는 다음과 같이 표현 가능하다.

이는 시간 Ts 마다 Sampling 한 신호이다.
Sampling 신호를 퓨리에 변환해주면 다음과 같다.

신호 -> sampling -> 퓨리에 변환 = 위의 사진 공식
표본화한 신호로부터 x(t)를 다시 복원 가능한 최저 표본화 주파수 fs = 2B를를 나이퀴스트율 이라고 한다.

[정리]
è 샘플링 신호를 만들기 위해서는 (기존 신호 x 임펄스 함수)를 해줌.
è 이를 퓨리에 변환하면 1/Ts 주기로 반복되는 주파수 영역에 대한 주기 함수로 정리된다.
è 다음 스펙트럼의 주파수가 2B(나이퀴스트율)이상이라면 원본 신호를 다시 복원 가능.
주파수 영역에서 신호 복원은 간단하다.
- 2B 이상으로 Sampling 시 Sampling 신호의 스펙트럼은 원래의 아날로그 신호 스펙트럼이 주파 수상에서 주기적으로 반복되는 (크기는 1/Ts 배) 형태
- 여기서 대역폭이 B Hz인 이상적인 LPF를 사용하면 원래의 신호와 동일한 스펙트럼을 얻을 수 있다.
- 이 필터의 전달 함수와 임펄스 응답은 다음과 같다.

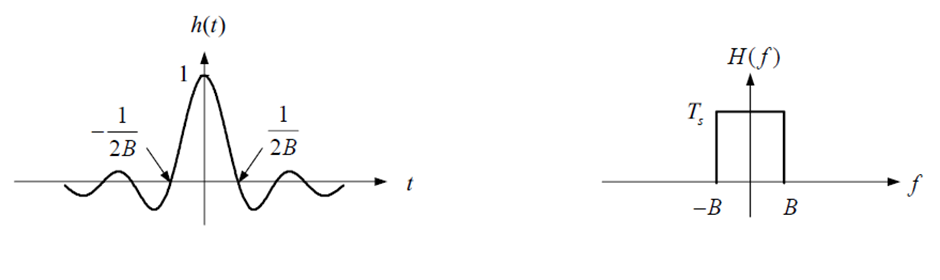
해당 그림 중 주파수 영역의 그림을 보면 2번째 줄의 내용을 의미함을 알 수 있다.
(그림만큼의 구간을 곱하면 원하는 주파수 영역의 구간이 나옴)
1. 0차 함수 = step function을 통해 근사화

[step function 시간 영역의 그래프는 sinc 형태로 주파수 영역이 결정된다.]

( xs(t) * h0(t) )를를 통해 우측 그림인 y(t)가 나타난다.

(시간 영역 & 주파수 영역의 식)
여기서 사용된 구형파는 간단하게 구현이 가능하기에 interpolation에서 주로 사용된다.

è 오차가 높음.
è sinc 의 낙차가 높아 주파수 축으로 검증가능.
è 이를 개선하고자 아래의 함수 사용
2. 1차 함수 = 선형 보간법 사용하여 오차 개선
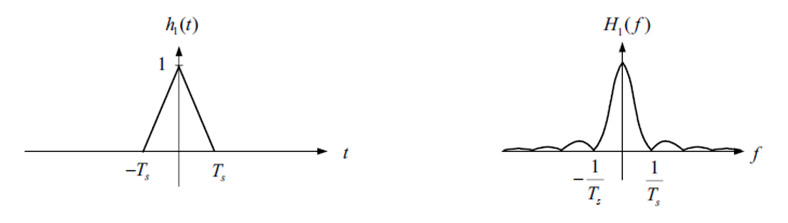
[linear 한 시간 영역의 그래프는 sinc2 형태로 주파수 영역이 결정된다.]
(삼각파 = linear interpolation)

여기서 다음 함수는 저항값 변화를 통해 제작이 가능하다.

(xs(t) * h0(t))를 통해 하단의 그림인 y(t)가 나타난다.

주파수 축의 오차 => 주파수 축의 H(f) 파형과 퓨리에 변환한(샘플링 신호)와 곱하여 나타나는 그림을 보면 sinc2 파형과 곱해졌기에, 원점 기준은 원본 신호를 잡을 수 있고, 그 외의 부분에서의 신호는 낮은 오차를 나타내게 된다.
3. 이상적인 interpolation = sinc함수 이용
=> 하지만 현실적으로 구현이 불가능한 파형이기에 사용은 불가하다.




è sinc의 퓨리에 변환 = 구형파
è 따라서 원하는 원본 신호를 정확하게 커팅 가능하다.
[정리]
è 전송된 아날로그 신호를 복원하기 위해 주파수 영역을 이용한다.
è 이때 대역폭이 B Hz인 이상적인 LPF 이용 시 원본 신호와 동일한 출력물을 얻을 수 있다.
è 가장 이상적인 보간 필터는 시간 영역에서의 sinc 파형이다.
è 하지만 이는 현실적으로 구현함에 어려움이 있기에, 구형파를 먼저 살펴보자.
è 구형파는 구현이 몹시 단순하지만 그만큼 많은 오차를 발생한다.
è 이는 주파수 영역을 통해 살펴보아도 확인 가능하다.
è 시간영역에서 주파수 영역(sinc 파형)으로 넘어가면 합성곱 -> 곱셈 으로 변함을 통해 살펴보면 출렁임이 크기에 오차가 많이 발생한다.
ð 이러한 오차를 개선하고자 선형 보간법을 이용한다.
ð 이는 저항값 변화로 제작이 가능하며, 주파수 영역에서 sinc^2 으로 나타나기에 출렁임이 확연하게 적음을 볼 수 있다.
ð 따라서 오차 발생이 훨씬 적음을 확인 가능하다.
[실제 환경에서의 문제점]
- 실제 환경에서 주어지는 신호는 시간은 제한적이며, 대역 제한되지 않는다.(aliasing 발생)
- Sampling을 적용할 수 있는 유한 대역폭 조건이 실제로 만족 될 수 없다.
- Sampling에서 사용한 임펄스열 신호는 물리적으로 구현 불가능 하다는 것이다.
Aliasing 현상을 없애기 위해서는 sampling 이전에 fs/2 이상의 성분을 제거하는 필터링 과정을 거치면 되지만 이는 구현 불가능하다.
실제로는 제거가 아닌 매우 작게 감쇄하는 높은 기울기의 차단 특성을 갖는 필터를 사용하여 약간의 스펙트럼 중첩이 발생한다.
따라서 Sampling 주파수를 필터 차단 주파수의 두 배(2B) 보다 조금 더 크게 잡는다.
'공부 > 통신' 카테고리의 다른 글
| [통신]디지털 변조의 원리 (ASK,PSK,FSK) (2) | 2022.10.29 |
|---|---|
| [통신] LPF & HPF & BPF (0) | 2022.10.20 |
| [통신] natural & flat-top sampling (0) | 2022.10.11 |