[실제 Sampling 과정]
실제 Sampling 과정에서 임펄스열 신호는 구현 불가능 하기에 유한 펄스폭을 지닌 구형 펄스열을 사용한다.
1. 자연 표본화(natural sampling)
ð 펄스의 폭은 일정하고, 아날로그 신호의 파형을 따라 변하도록 하는 방식.

그림에서 사용된 구형 펄스열에서 원점에 위치한 한 주기의 구형 펄스가 p(t)이고 이를 식으로 나타내면 다음과 같다.
이때, 구형 펄스파 사용 이유는 임펄스는 실질적으로 구현 불가하기에 대체 신호로 사용하기 위해이다.


이후 Ts 주기로 반복하여 생성한 구형 펄스열을 퓨리에 변환으로 나타내면 다음과 같다.

다음 과정으로 나온 P(nfs) 에는 구형 펄스파의 퓨리에 변환 값을 대입

이때 cn 값에 의해서 주파수 영역에서 임펄스열의 크기는 일정하지 않다.
주파수 영역에서 임펄스열 => 퓨리에 변환을 한 (sinc x 임펄스열)
최종적인 Natural Sampling 신호의 퓨리에 변환은 다음과 같다.
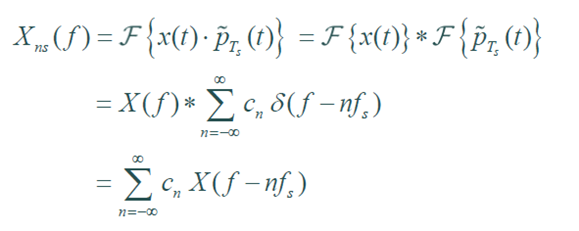
è 원본 신호의 스펙트럼 모양이 주기적으로 반복되는 것은 이상적인 임펄스 sampling과 유사하다.
è 임펄스 Sampling 에서는 동일한 이득이 곱해져 반복되지만, Natural Sampling에서는 X(f)에 cn이 곱해져서 반복된다는 차이점이 존재
è fs > 2B 가 되도록 선택 시 스펙트럼 중첩이 발생하지 않는다.
è 메시지 신호(원본 신호)를 따라간다.

sinc 파형은 n의 값(다른 이득)에 따라서 주파수 영역의 임펄스파 값이 다르게 나온다.
최종적으로 나타난 주파수 영역의 그림을 보면 원점 근방의 원본 메시지만 가져가면 실제Sampling 과정이 완성된다.
è p(t)= (임펄스파 * 구형파)
è x(t) x p(t) = natural sampling
2. 평탄 표본화(flat – top sampling)
ð 펄스의 진폭이 표본화 순간의 아날로그 신호의 값으로 펄스 구간 동안 일정하게 유지되는 방식


구형 펄스파의 진폭을 펄스 구간 중앙에서의 신호 값으로 한다.
Flat – top = (원본 신호 x 델타(Ts) 주기로 반복) * 구형파
ð 주파수가 높은 범위에서 신호 왜곡이 된다. (해결하기 위해서는 타우를 줄여줌)

델타 * 구형파 = p(t - nTs)
è 이는 flat-top sampling 신호의 스펙트럼이다.
è 따라서 원본 신호의 스펙트럼 X(f)와 달라진다.
è 타우(펄스 폭)가 작을수록 스펙트럼 변화가 작게 일어난다.
P(t) 와 델타 가 convolution 하기에 1이상의 값이 나올 수 도 1이하의 값이 나올 수도 있다.
따라서, 다음과 같은 sampling 신호가 곱해지므로 filtering 효과로 인해 high frequency loss 가 있다.
이를 해결하기 위해서는,
1. PAM신호의 대역폭이 넓어지기에 타우를 작게 선택한다. (but, 이는 delta function을 만든다는 뜻이기에 불가능하다.)
2. 고주파쪽 gain을 크게 하는 equalization filter 사용.
Flat – top 방법을 사용하는 것 또한 문제는 없지만, 주파수 0의 위치 이외의 부분을 filtering 하면 왜곡이 발생한다.
[실제의 여파기]
힘(전력)은 제곱의 단위를 갖는다. [P = I^2R = V^2/R]
10log10(P2/P1) = dB (전력 = P)
10log10(2) = 3.xx[dB]에 근접한다. 10log10(4) = 6[dB]
따라서 대략 3dB이라고 가정하였을 때, 3dB의 차이는 2배의 차이를 지님을 유추 가능하다.
이의 반대인 -3dB 지점은 1/2배의 차이가 나는 것을 알 수 있다.
3dB 대역폭 (filter의 대역폭) = 최대 응답치의 -3dB 지점을 경계로 한다.

이는 -3dB 지점에서 입력 신호의 반을 깎아 주게 된다.
이후 주파수가 커질수록 신호가 점점 덜 통과하는 형태를 보여준다.
본래 이상적인 LPF는 델타f 지점에서 칼로 자르듯 딱 떨어지지만 이는 현실적으로 구현 불가능한 방식이기에 다음과 같은 방법을 통해 표현한다.

이후의 다른 신호들 또한 위의 LPF와 동일하게 -3dB과의 교차점이 중요하기에 해당 주파수를 알아내는 것이 중요하다고 볼 수 있다.
'공부 > 통신' 카테고리의 다른 글
| [통신]디지털 변조의 원리 (ASK,PSK,FSK) (2) | 2022.10.29 |
|---|---|
| [통신] LPF & HPF & BPF (0) | 2022.10.20 |
| [통신] Sampling 과정 (2) | 2022.10.10 |