8.1 pn 접합 전류 / 경계조건

 

 

forward bias에서 pn 접합의 전위 장벽이 줄어 전류가 흐른다는 것을 이전의 장을 통해 확인하였다.

pn junction in forward bias

 

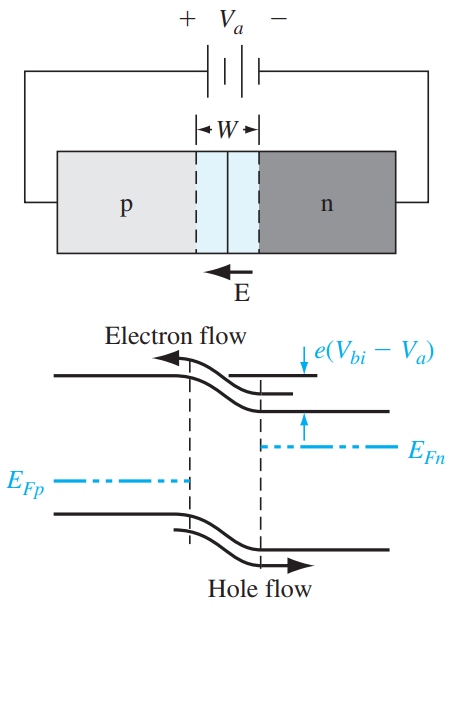
이때의 전자 흐름을 살펴보면, (괄호 안의 기준은 전자와 정공을 기준으로)

1) 전자가 N(major) -> P(minor)로 건너간다.

2) depletion region 경계면에서 전자의 농도가 가장 높고, 반대로 경계면과 거리가 먼 부분의 농도는 낮다.

3) 농도가 높은 영역에서 낮은 영역으로 확산되며 전자가 점차 이동(확산)한다.

4) P 영역은 hole이 major carrier이므로 이동한 전자들과 결합하며 확산을 하기에 전자의 농도는 점차 감소하고 최종적으로 $n_{p0}$ 열평형 상태에서의 농도까지 감소한다.

 

이 상황의 반대가 정공 흐름 이란 유추 가능하다.

 

여기서 $J_{n}(x)$ & $J_{p}(x)$ 에 대한 Current는 위치에 따라 다른 값을 갖지만, 앞장에서 확인하였듯 $J_{total} = J_{n}(x) + J_{p}(x)$ 인 $J_{total}$ 값은 항상 일정하게 유지되어 한 개의 carrier 값을 찾는다면 다른 carrier의 값 또한 확인 가능하다.

 

728x90

 

---

이렇게 살펴본 minority carriers의 농도의 확산을 그래프로서 확인을 해보면 아래와 같다.

 

Minority carriers 농도의 그래프 (좌 : $J_{n,diff}$ , 우 : $J_{p,diff}$)

 

depetion region 경계면에서 excess carrier의 농도가 가장 높다.

여기서 excess carrier란, p-type의 경우 n-type으로부터 넘어온 전자를 말한다. 마찬가지로 n-type의 경우는 정공을 이야기한다.

이렇게 생성된 excess carrier 들은 각 타입에서의 major carrier와 recombination 되어 이동함에 따라 사라지고 결국 열평형 상태에서의 농도($n_{p0}$ , $p_{n0}$)까지 감소한다.

 

majority carrier 가 아닌 minority carrier 만 고려하는 이유는, 직전 포스팅이었던 기본 가정들 중 low level injection 이 존재했기 때문이다.

만약 major 농도를 대상으로 보면 n 타입에서 전자가 들어와도 majority carrier에는 큰 영향을 주지 않고 열평형 상태에서의 농도와 같기에 minority carrier만 고려한다.

---

이렇게 알아본 carrier 의 농도를 살펴보자.

 

$n_{n0} ~ N_{d}$ , $p_{n0} = \frac {n_{i}^{2}}{N_{d}}$ 
$p_{p0} ~ N_{a}$ , $n_{p0} = \frac {n_{i}^{2}}{N_{a}}$

 

이렇게 나온 두 개의 농도 공식을 $V_{bi}$ 에 대입을 한다.

이를 정리해주면

열평형 상태에서의 농도 공식

 

 다음과 같은 ($n_{n0} , n_{p0}$ & $p_{p0} , p_{n0}$) 연관성을 지닌 수식이 확인 가능하다.

열평형 상태에서의 캐리어 농도 표기

 

여기서 forward bias를 인가하였기에 열평형 상태가 아님으로,

forward bias 인가된 농도 공식

0을 지워주고, $V_{bi}$ 대신 인가한 forward 전압만큼 뺀 값을 넣어준다.

 

하지만, 우리는 low level injection을 통해 major carrier 농도는 크게 변하지 않는다는 것을 가정할 수 있었다. 따라서 $n_{n} ~ n_{n0}$ , $p_{p} ~ p_{p0}$로 변경한 식을 적어준다.

 

forward bias 인가된 carrier 농도 (열평형 상태 농도로 가정)

 

 

320x100

 

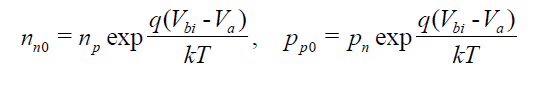
열평형 상태로 정리되었던

열평형 상태에서의 농도 공식

 

이 식과 서로 같다고 놓으면 

 

$n_p = n_{p0} exp\frac {qV_{a}}{kT}$

$p_n = p_{n0} exp\frac {qV_{a}}{kT}$

로 정리된다.

 

---

 

각 타입별 캐리어의 농도

 

위에서 정리된 수식에서 $n_{p}$ 와 $p_{n}$은 서로 건너온 캐리어(전자 , 정공)의 농도도 더해준 값을 이야기한다.

 

 

따라서 depletion region 인 $-x_p , x_n$ 에서 농도값을 최대로 갖고, forward bias를 많이 가할수록 값이 증가한다는 것을 유추할 수 있다.

 

마지막으로 다음 그림을 통해

 

순수하게 n-type & p-type으로 건너온 excess carrier 값을 구하는 수식을 살펴보겠다.

 

먼저 $n_{p0}$ 와 $p_{n0}$ 두 값은 원래 있던 열평형 상태에서의 전자와 정공 값임을 알 것이다.

따라서 해당 부분을 제외한 농도 값이 바로 순수하게 넘어온 excess carrier 값이 된다.

 

순수한 excess carrier 농도

 

결국 끝에서는 열평형 상태의 농도에 도달하니 excess carrier가 무한대로 가면 0으로 수렴하는 값을 갖는다.