연속 신호의 지수함수는 x(t)=Ceatx(t)=Ceat로 나타난다.
여기서 a, 와 C의 값이 실수인지 복소수인지에 따라 달라진다.
- 실수 (a , C)

C와 a 모두 실수의 값을 갖고 있을 경우 a>0 에서는 증가하는 그래프를, a <0 에서는 감소하는 그래프를 그린다.
- 복소 지수
이는 x(t)=Ceatx(t)=Ceat 에서 승수가 복소수일 때를 말한다. (a=jω0a=jω0)
ω0ω0 = 각속도 (ω0<0ω0<0 = 시계 반대 방향 , ω0>0ω0>0 = 시계 방향)

x(t)=ejω0tx(t)=ejω0t (C=1이라 가정) 여기서 오일러 공식을 사용하여
x(t)=cosω0t+jsinω0tx(t)=cosω0t+jsinω0t 로 나온다. 이때의 주기는 2π|ωo|=T02π|ωo|=T0로 구할 수 있다.
우리는 주기 함수의 정의를 통해
ejω0(t+T)=ejω0tejω0T=ejω0tejω0(t+T)=ejω0tejω0T=ejω0t 가 만족한다면 주기 함수임을 확인 가능하다.
해당 수식을 만족하기 위해서는 ejω0T=1ejω0T=1 이 만족되어야 한다.
그러므로 T0=2π|ωo|T0=2π|ωo| 을 대입하여 주면 θ=ω0tθ=ω0t 수식을 이용해 θθ 대신 2π2π가 들어가며 x축에 mapping이 된다. 그리고 해당 식의 반지름이 1을 갖기에 정리된 값도 실수 값 1로 나타난다.
ejω0Tejω0T에서 ej2π=1ej2π=1
ejω0t=ejω0(t+T)ejω0t=ejω0(t+T) 의 주기 함수가 나타난다.
따라서 x(t)는 기본 주기가 T0T0인 주기 함수이다.
ejω0t=cosω0t+jsinω0tejω0t=cosω0t+jsinω0t
e−jω0t=cosω0t−jsinω0te−jω0t=cosω0t−jsinω0t
cosω0t=12(ejω0t+e−jω0t)cosω0t=12(ejω0t+e−jω0t)
sinω0t=12(ejω0t−e−jω0t)sinω0t=12(ejω0t−e−jω0t)
지수 부호성분에 따라 허수 성분이 바뀐다.
x(t)=Acos(ω0t+φ)x(t)=Acos(ω0t+φ)
위상(φφ)의 존재함으로서 회전한 위치부터 식(원)이 시작한다.
위상을 적용한 식을 다시 정리하면
Acos(ω0t+φ)=A2ejφejω0t+A2e−jφe−jω0t=ARe{ej(ω0t+φ)}Acos(ω0t+φ)=A2ejφejω0t+A2e−jφe−jω0t=ARe{ej(ω0t+φ)}(실수부)
Asin(ω0t+φ)=A2ejφejω0t−A2e−jφe−jω0t=AIm{ej(ω0t+φ)}Asin(ω0t+φ)=A2ejφejω0t−A2e−jφe−jω0t=AIm{ej(ω0t+φ)}(허수부)
로 나타난다.
복소 지수 신호에서의 Energy 와 Power는 주어진 신호의 대표하는 값을 수치화로서 표현하고자 사용한다.
Energy는 무한한 값과 유한한 값을 가지나 무한한 값은 필요성이 없고, Power의 경우 유한한 값을 갖게 된다.
E=∫t2t1|x(t)|2dtE=∫t2t1|x(t)|2dt = 여기서 |x(t)|는 절댓값이 아닌 크기이다.
ejω0t=cosω0t+jsinω0tejω0t=cosω0t+jsinω0t
로 정의된 다음 수식을 통해 Eperiod,PperiodEperiod,Pperiod값을 구해보자.
Eperiod=∫T00|ejω0t|2dt=∫T001dt=T0Eperiod=∫T00|ejω0t|2dt=∫T001dt=T0 로 나타난다.
(|ejω0t|=1|ejω0t|=1의 크기(magnitude)를 지님.)
Pperiod=1T0Eperiod=1Pperiod=1T0Eperiod=1이다.
(Eperiod=T0Eperiod=T0 의 값을 지니므로 결괏값이 1로 나오게 된다.)
연속신호
C&a = Complex number C=|C|ejθC=|C|ejθ, a=r+jω0a=r+jω0
a값을 θθ에 대입하여 식을 전개하면,
Ceat=|C|ejθe(r+jω0)t=|C|ertej(ω0t+θ)Ceat=|C|ejθe(r+jω0)t=|C|ertej(ω0t+θ)
로 나타난다.
앞의 |C|ert|C|ert 부분은 실수 부분으로 r에 따라 변화하며 크기 값에 영향을 준다.
반대로 ej(ω0t+θ)ej(ω0t+θ) 는 복소수 부분으로 크기 값에 영향을 주지 않는다.

Ceat=|C|ert(cosω0t+θ)+j|C|ert(sinω0t+θ)Ceat=|C|ert(cosω0t+θ)+j|C|ert(sinω0t+θ)
이산 신호
연속에서와는 다르게 x[n]=Cαnx[n]=Cαn으로 표현한다.
이는 e(an)e(an)의 경우 항상 양의 값을 갖기에 정보가 제한적인 반면 αnαn의 경우 음수도 지닐 수 있어 더 많은 정보를 나타낼 수 있다.
하지만 연속에서는 사용불가능하다.
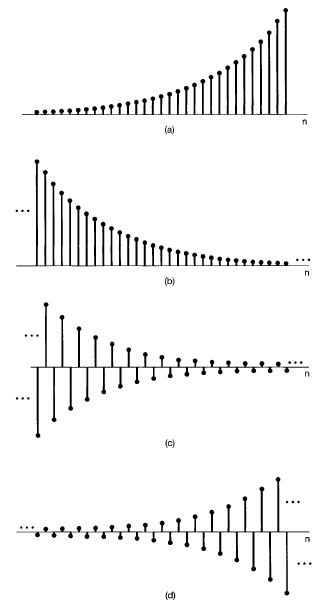
a) C>0 , alphaalpha>1 (점차 증가)
b) C>0 , 0 <alphaalpha<1 (점차 감소)
c) alphaalpha<0 , |alphaalpha| < 1 (와리가리 하면서 감소)
d) alphaalpha<0 , |alphaalpha| > 1 (와리가리 하면서 증가)
C & D 그림의 경우 음과 양의 값을 왔다 갔다 하는 형태로 그려지기에 CT(연속 신호)에서는 사용 불가능하다.
DT의 기본 주기 N0N0값을 구해보자.
먼저 ejω0(n+N)=ejω0nejω0N=ejω0nejω0(n+N)=ejω0nejω0N=ejω0n 가 만족 시 정의에 의해서 주기가 n 인 주기 함수가 된다.
해당 값을 만족하기 위해서는 ejω0N=1ejω0N=1 이 돼야 한다.
그러므로 ω0N=2πmω0N=2πm (m=정수배)가 되고, N=2πω0×mN=2πω0×m이다.
여기서 m은 N이 정수가 되도록 만드는 최소 정수 값을 뜻한다.
예를 들어,
x[n]=cos2π12nx[n]=cos2π12n 에서 기본 주기를 구하는 방법은
1. ω0n=2π12n=2πmω0n=2π12n=2πm 이므로 ω0nω0n이 2πm2πm이 되기 위한 최소 m을 구한다.
2. n=12mn=12m 임을 확인하였고 이게 정수가 되기 위한 최소 m 값은 1로 나타난다.
3. 그러므로 기본 주기 N0=12N0=12가 된다.
따라서 다음 사진과 같이 연속 & 이산 신호에 관한 식이 정리가 된다.

해당 수식을 이용하여 아래 사진의 이산 신호의 기본 주기를 확인해보자.
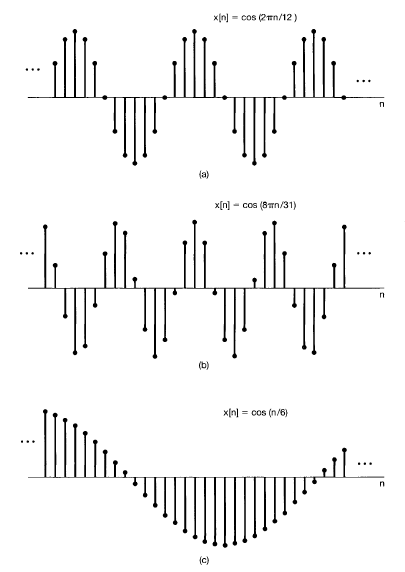
a) ω0=2π12ω0=2π12
2π12n=2πm2π12n=2πm , n=12mn=12m , N0=12N0=12
m = 1 (정수) 값으로 나오므로 기본 주기 값 N0=12N0=12이다.
b) ω0=8π31ω0=8π31
8π31n=2πm8π31n=2πm , n=314mn=314m , N0=314
m = 1 (정수)에서 N0 값이 정수로 나오지 않는다. 따라서 기본 주기가 정수 값으로 나오는 최소 정수인 m = 4에서의 기본 주기 값 N0=31이다.
c) ω0=16
16n=2πm , n=12πm , N0= 정수 불가능 (주기 신호 X )
본래 연속 신호에서는 주파수가 낮은 파형의 주기가 더 높게 나온다. (주기 ↑ 주파수 ↓ or 주기 ↓ 주파수 ↑)
하지만 이산 신호에서는 그렇지 않은 경우도 존재한다.
위의 경우를 살펴보면 주파수가 a보다 b가 크기에 CT의 경우 주기가 b < a로 나타나야 하지만 DT에서는 a < b의 경우로 존재한다.
'공부 > 신호 및 시스템' 카테고리의 다른 글
| 1.3 이산 신호의 주기성 + 1.4 단위 계단 함수 (0) | 2022.02.05 |
|---|---|
| 1.2 우함수 & 기함수 (0) | 2022.02.03 |
| 1.1 연속 신호 와 이산 신호 (0) | 2022.02.02 |