앞장에서 보았듯, CT에서의 주파수 증가는 양과 음을 더 빠르게 왕복하며 주기가 짧아지게 된다.
그렇다면 주파수 증가에 따른 주기의 감소 현상이 이산 신호에서도 적용되는지 확인해보도록 하자.
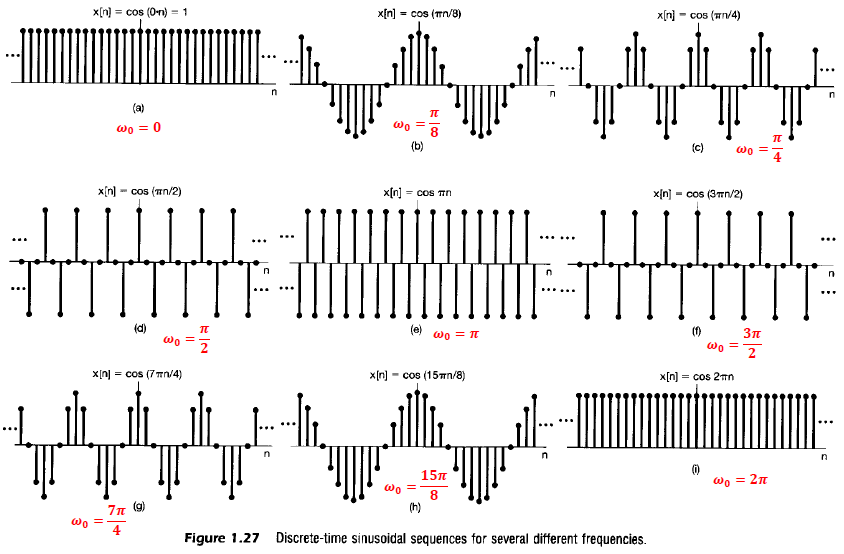
위의 사진에서 몇 가지를 뽑아서 살펴보면
b) $\frac {\pi}{8} n = 2\pi m$ -> $n = 16m$ (이때 m=1이라는 최소 정수가 들어감으로) $N_{0} = 16$ 이 기본 주기가 된다.
c) $\frac{\pi}{4}n = 2\pi m$ -> $n = 8m$ (이때 m=1이라는 최소 정수가 들어감으로) $N_{0} = 8$ 이 기본 주기가 된다.
다음과 같은 과정을 통해 살펴보니 주파수 증가에 따른 주기가 감소함을 확인할 수 있다.
하지만,
e) 를 기점으로 살펴보면,
f) $\frac{3\pi}{2}n = 2\pi m$ -> $n = \frac {4}{3} m$ (이때 m=3이라는 최소 정수가 들어감으로) $N_{0} = 4$ 이 기본 주기가 된다.
g) $\frac{7\pi}{4}n = 2\pi m$ -> $n = \frac {8}{7} m$(이때 m=7이라는 최소 정수가 들어감으로) $N_{0} = 8$ 이 기본주기가 된다.
주파수가 증가함에 따라 주기가 다시 증가함을 볼 수 있다.
이는 0 ~ $2\pi$ 주기로 반복적으로 나타나며 해당 주기 내에의 신호들은 모두 다르게 나타난다.(DT에서)
수식적으로 표현하면, $e^{j(\omega_{0} + 2\pi) n}=e^{j\omega_{0} n} e^{j2\pin}=e^{j\omega_{0} n}$이다.
이때 물리적으로 가장 높은 주파수를 띠는 값은 (e)이고, $e^{j\pi n}=(e^{j\pi})^{n} = (-1)^{n}$ 의 값을 갖는다.
따라서 정리를 하면,
CT
$cos(\omega_{0} t)$ ($-\infty < \omega_{0} < \infty$) <- 각각이 전부 다른 신호를 갖는다.
그러므로 $\omega_{0}$가 모든 구간에 대해 주기 신호의 의미가 존재하고,
$\omega_{0}$가 커질수록 신호에서 진동의 비율이 높아진다.
DT
$cos(\omega_{0} n)$ ($0 < \omega_{0} < 2\pi$) or ($-\pi < \omega_{0} < \pi$)
$cos(\omega_{0} + 2\pi) n = cos(\omega_{0} n)$ : 해당 결과 값은 틀리지만 주기 신호이기에 물리적 특성의 신호는 같다.
1.4 단위 계단 함수
단위 계단 함수는 n=0 일때만 크기 1을 지니는 함수이다. (DT)
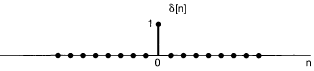

따라서 n의 값을 이동시켜 $\delta[n-1]$ 일때는


로 나타난다.
이를 일반화 시키면, n-k 혹은 n+k 만큼 이동시킨 델타 함수는 다음과 같이 표현되며,

델타함수는 $\delta[n] = u[n] - u[n-1]$ 로 정리된다.
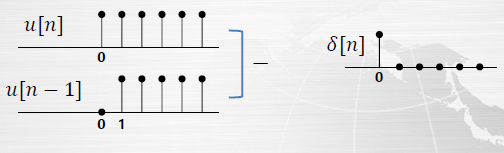
그러므로 이러한 unit step function은 delta function의 합으로 이루어진다.

- Sampling & Unit Sample Signal
$x[n]\delta[n] = x[0]\delta[n] = x[0]$
해당 식의 경우 n = 0 일때만 $\delat[n]$이 1의 값을 갖고 나머지는 0 을 갖는다.
이걸 통해 $x[0]$의 값만 뽑아낼수있다.
이를 일반화한 식으로 살펴보면,
$x[n]\delta[n-n_{0}] = x[n_{0}]\delta[n-n_{0}] = x[n_{0}]$
다음과 같이 $n = n_{0}$ 일때만 $\delat[n]$이 1의 값을 갖고 나머지는 0 을 갖는 식으로 정리가 된다.
위에서 본 DT에서와 동일하게 단위 계단 함수는 t=0 일때만 크기를 지니는 함수이다. (CT)
다만, CT에서의 delta fucntion = Dirac delta function 으로 불리며, t=0 에서 1의 크기가 아닌 무한대의 크기를 갖는다.

그리고 CT에서는 delta function을 $u[n]$의 차로 나타내었지만, DT에서는 $\delta(t) = \frac{du(t)}{dt}$ 인 미분을 사용하여 delta function을 나타낸다.
따라서 $u(t)$의 값을 구하기 위해서는 Sigma가 아닌 적분기호를 사용하여 나타냄.
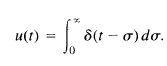
- Sampling & Unit Sample Signal
DT에서와 동일하게 해석 가능하다.
0에서만 의미있는 구간을 지니므로 다음과 같은 식으로 정리가 된다.
$x(t)\delta(t) = x(0)\delta(t)$
$x(t)\delta(t-t_{0}) = x(t_{0})\delta(t-t_{0})$
'공부 > 신호 및 시스템' 카테고리의 다른 글
| 1.3 Exponential and sinusoidal signal (0) | 2022.02.03 |
|---|---|
| 1.2 우함수 & 기함수 (0) | 2022.02.03 |
| 1.1 연속 신호 와 이산 신호 (0) | 2022.02.02 |